أنماط التعلم - ما هي أنماط التعلم لدى المتعلمين

مفاهيم احصائية - المتغير العشوائي البرنولي_ البواسوني_ المنتظم والأسي.

في علم الاحتمالات والإحصاء. تعتبر الفهم الصحيح لأنواع المتغيرات العشوائية أمرًا أساسيًا. فالمتغيرات العشوائية هي مفتاح فهم الظواهر التي يمكن تمثيلها بشكل عشوائي. وتلك الظواهر تتنوع بحسب طبيعتها وتوزيعاتها.

لنبدأ بالمتغير البرنولي. وهو من أبسط أشكال المتغيرات العشوائية. يمكن وصف المتغير البرنولي بأنه يتبع توزيع برنولي إذا كان لديه اثنتان فقط من النتائج المحتملة: نجاح أو فشل. على سبيل المثال. رمي عملة معتمدة حيث يكون هناك احتمال للحصول على وجه أو ختم. هذا المتغير يُمثل بشكل عام بواسطة القيم 0 و 1. حيث يكون 1 للنجاح و 0 للفشل.

أما المتغير البواسوني. فيشير إلى توزيع الاحتمالات الذي يصف عدد الأحداث التي تحدث في فترة زمنية محددة عندما يكون الوقوع المتوقع لكل حدث ثابتًا. وغالبًا ما يُرمز له برمز "λ" (لامبدا). يتم تمثيل قيم المتغير البواسوني بأعداد صحيحة غير سلبية فقط. ويستخدم على نطاق واسع في تحليل العمليات التي تشمل العد التكراري للأحداث مثل وقوع الزلازل. وعدد الزوار في متجر معين خلال ساعة محددة. وما إلى ذلك.

أما المتغير المنتظم. فهو ينتج عن عملية توزيع عادلة ومتجانسة للفرص. حيث يكون كل نتيجة ممكنة للظاهرة ذات احتمال متساوية للحدوث. كما هو الحال مع رمي النرد. حيث يكون لكل وجه من أوجه النرد احتمال متساوٍ للظهور.

أخيرًا. المتغير الأسي يشير إلى المتغير العشوائي الذي يتبع توزيعًا معياريًا معينًا يُعرف بالتوزيع الأسي. والذي يمكن وصفه بشكل أساسي باستخدام معادلة كثافة الاحتمال الخاصة به. وهو يستخدم على نطاق واسع في الإحصاء لنمذجة الأحداث التي تنتج عنها توزيع ذو شكل معين مثل التوزيع الطبيعي أو التوزيع الجاما.

بهذا. يتبين أنه على الرغم من أن كل من هذه المتغيرات العشوائية تختلف في طبيعتها واستخداماتها. إلا أن فهمها يساعد في فهم أوسع للظواهر العشوائية التي تحدث في العالم الحقيقي.


تعريف المتغير العشوائي.

هو متغير مجهول القيمة، يستخدم عند دراسة الظواهر العشوائية، مثل رمي حجر النرد، فتكون النتائج المتوقعة هي ما يعبر عنه بالمتغير العشوائي (خضرة، د - ت، ص1).

الفرق بين المتغيرات العشوائية.

1. المتغير العشوائي البرنولي: وسمي بهذا الاسم نسبة لمكتشفه " جيمس برتوللي". ويسمى بمحاولات برنوللي، يتميز بالخصائص التالية: (النعيمي وطعمة، 2020، ص 109). وهو متغير عشوائي ثنائي النتيجة، أي يمكن أن يأخذ قيمتين فقط: (صفر وتمثل حالة الفشل) أو (واحد وتمثل حالة النجاح). ويمثل تجربة ثنائية النتيجة، مثل رمي القطعة النقدية (رؤوس أو كتف). له دالة كتلة احتمالية محددة بقيمتي n (عدد النجاحات) و p (احتمال النجاح) واحتمال الفشل (q = 1-p). مثال: رمي العملة المعدنية 10 مرات وعدد مرات ظهور "رؤوس".
2. المتغير العشوائي البواسوني: وسمي بهذا الاسم نسبة لمكتشفه " سايمون بواسون" . وله أهمية كبيرة في التطبيقات الإحصائية المتعددة، ويستخدم في المجالات الإدارية وبحوث العمليات، لأنه العامل الأساسي في بناء نماذج نظرية صفوف الانتظار. ويطبق عليه " توزيع الحوادث النادرة الوقوع". يتميز بالخصائص التالية: (النعيمي وطعمة، 2020، ص 109). وهو متغير منفصل يمثل عدد الأحداث أو محاولات النجاح التي تحدث في فترة زمنية معينة أو على مساحة محددة. ويفترض أن الأحداث تحدث بشكل مستقل عن بعضها البعض وبمعدل ثابت. له دالة كثافة احتمالية محددة بقيمة أو معلمة λ (معدل الأحداث). مثال: عدد المكالمات الهاتفية التي تلقاها مركز خدمة العملاء خلال ساعة. عدد الزبائن الذين يدخلون البنوك خلال (15) دقيقة.
3. المتغير العشوائي المنتظم: هو متغير متصل يمكن أن يأخذ أي قيمة ضمن نطاق محدد. ويمثل ظاهرة عشوائية ذات قيم متصلة، مثل طول شخص ما أو وزن قطعة فاكهة. له دالة كثافة احتمالية محددة بقيمتي a و b (حدود النطاق). (طويطو، 2017، ص37). مثال: قياس أطوال الطلاب في فصل دراسي. أو أوزان طلاب مدرسة معينة
4. المتغير العشوائي الأسي: ويستخدم لمعالجة بعض التطبيقات الإحصائية الخاصة بالمتغيرات العشوائية.  وهو متغير متصل يمثل الوقت الذي يستغرقه حدوث حدث معين. يفترض أن احتمال حدوث الحدث ثابت في أي لحظة زمنية. له دالة كثافة احتمالية محددة بقيمة 0 < λ (معدل الحدوث). مثال: مدة انتظار شخص في طابور الانتظار. أو طول فترة الانتظار في صف انتظار عند الإشارة الضوئية (النعيمي وطعمة، 2020، ص 109).

ملخص للمقارنات السابقة بين أنواع المتغيرات العشوائية نوضحه في الجدول التالي:

المراجع.

1. النعيمي، محمد عبد العال وطعمة، حسن ياسين. (2020). الإحصاء التطبيقي. عمان: دار وائل للنشر والتوزيع. تم الاسترجاع من الرابط https://platform.almanhal.com/Details/Book/95.
2. خضرة ، راشدي. (د - ت). المتغيرات العشوائية والتوزيعات الاحتمالية. المحاضرة 6 و7 مادة الإحصاء الرياضي وتطبيق الاختبارات الإحصائية. ماستر 1. يموغرافيا اجتماعية. كلية العلوم الاجتماعية. جامعة وهران 2 محمد بن أحمد. الجزائر. ملف pdf. تم الاسترجاع من الرابط https://elearn.univ-oran2.dz/pluginfile.php/201219/mod_resource/content/2/%D8%A7%D9%84%D9%85%D8%AA%D8%BA%D9%8A%D8%B1%D8%A7%D8%AA%20%D8%A7%D9%84%D8%B9%D8%B4%D9%88%D8%A7%D8%A6%D9%8A%D8%A9%20%D8%A7%D9%84%D9%85%D8%AD%D8%A7%D8%B6%D8%B1%D8%A9%20%205%20%D9%886.pdf
3. طويطو، محمد. (2017). مطبوعة خاصة بمقياس: الإحصاء 3. موجهة لطلبة السنة الثانية ليسانس جميع الشعب. كلية العلوم الاقتصادية والعلوم التجارية وعلوم التسيير. جامعة الجزائر 3.

---------------------------------------------------------------------------

الواجب الكتابي . الاحتمالات

في البداية يمكننا تعريف الاحتمال بأنه إذا كان لدينا A حدثاً من Ω فإن احتمال وقوع الحدث ورمزه P(A) يعطى بالعلاقة (بوساحة، 2008، ص110).

p(A) = m/n

حيث m عدد الإمكانات الملائمة لوقوع الحدث A.

N هو عدد الإمكانات الكلية للتجربة

إذا كان احتمال أن يصاب مدخن ما بمرض في الرئة هو ٠٫١٨ وتم فحص ١٠٠٠ مدخن، احسب التالي:

١. ماهو عدد الأشخاص المتوقع أن يكونوا معانين من مرض الرئة.

الاحتمال: نسبة المصابين P = 0.18
عدد المدخنين: وهو حجم العينة N = 1000
عدد الأصحاء Q : 1-0.18 = 0.82

الحل.
العدد المتوقع: 0.18 * 1000 = 180 شخص (MX=N*P)

٢. ماهو الانحراف المعياري لعدد الأشخاص الذين من الممكن أن يصابوا بمرض في الرئة

الاحتمال: 0.18
عدد المدخنين: 1000

الحل.

التباين = S^2=N*P*Q

التباين = 1000*0.18*0.82 = 147.6
الانحراف المعياري = الجذر التربيعي للتباين: √ (0.18 * 0.82 * 1000) = √(147.6) = 12.149

٣. ماهو احتمال أن نجد أكثر من ١٣٥ شخص مصاب بمرض في الرئة

الاحتمال: 0.18
عدد المدخنين: 1000
عدد الأشخاص المراد حساب احتمالية وجودهم: 135

الحل.

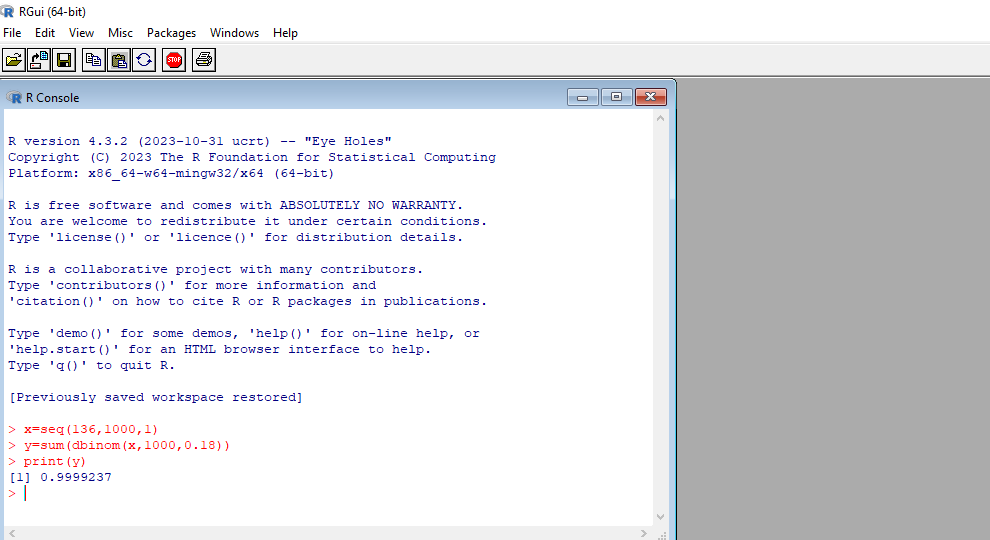
من خلال برنامج R نجد أن احتمالية أن نجد عدد الأشخاص المصابين بمرض في الرئة يزيد عن 135 هو 0.9999237 كما هو مبين في المخطط التالي

٤. ماهو احتمال أن يكون عدد الأشخاص المصابين يتراوح بين ١٦٥ و ١٤٠ شخص؟

الاحتمال: 0.18
عدد المدخنين: 1000
عدد الأشخاص المراد حساب احتمالية تواجدهم هو : 165 – 140 = 25 .

الحل.

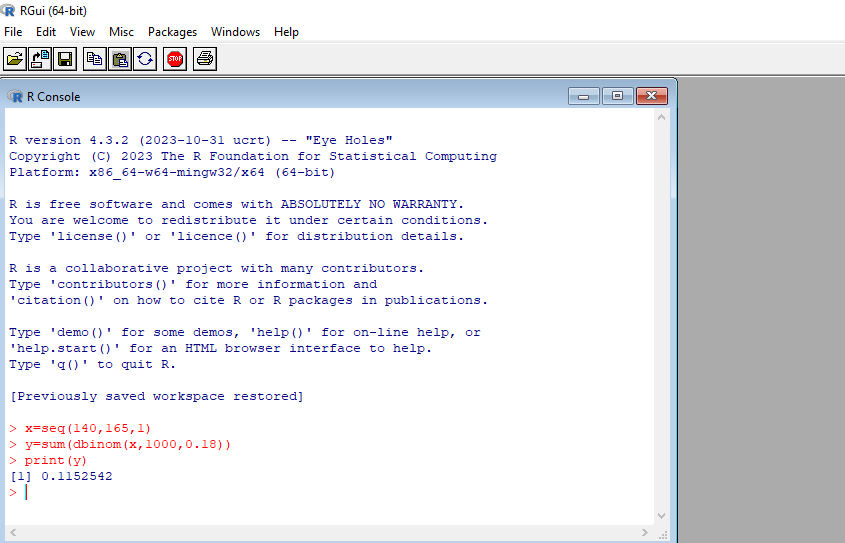
من خلال استخدام برنامج R الإحصائي لحساب احتمالية أن يكون عدد الأشخاص المصابين ضمن هذا المجال هو 0.1152542، كما هو مبين في المخطط التالي

في الختام يمكن القول تعتمد هذه الحسابات على افتراض أن احتمال إصابة كل مدخن بمرض في الرئة هو 0.18، ولكن في الواقع، قد يختلف هذا الاحتمال اعتمادًا على عوامل أخرى مثل العمر والجنس وعدد السجائر المدخنة.

المراجع.

1. بوساحة، حورية. (2008). الإحصاء والاحتمالات. المعهد الوطني لتكوين مستخدمي التربية وتحسين مستواهم. الجزائر. تم الاسترجاع من الرابط https://sites.pitt.edu/~super1/ResearchMethods/Arabic/statsticalbookinarabict.pdf.

---------------------------------------------------------------------------

مجلة التعلم.

بالطبع! يُعتبر نظام الترحيل أحد المفاهيم الرئيسية في الإحصاء، ويُستخدم لفهم وتحليل البيانات المجمعة. يشير نظام الترحيل إلى العملية التي يتم فيها ترتيب البيانات بشكل منظم وتصنيفها حسب قيم معينة أو فئات. يتم ذلك لفهم توزيع البيانات والمعلومات المتاحة بشكل أفضل، وللكشف عن الأنماط والاتجاهات الكامن

التمرين الأول.

حدد نوع التوزيع الذي نلجأ له في كل من الحالات الآتية:

1. فحص 400 مصبح في مصنع إن كانت تالفة أم لا.

نوع التوزيع: هو التوزيع الثنائي (ذو الحدين)، والسبب لأنه (طويطو، 2017، ص18):

➰ لدينا تجربة عشوائية (فحص المصباح) مع نتيجتين محتملتين (تالف / سليم).

➰ عدد التجارب ثابت (400 مصباح).

➰ احتمالية النجاح (المصباح سليم) ثابتة لكل تجربة.

➰ التجارب مستقلة عن بعضها البعض.

2. عدد قطرات المطر التي ستسقط على شريط كهربائي ممدد بين منزلين.

نوع التوزيع: توزيع بواسون، والسبب لأنه (طويطو، 2017، ص18):

➰ لدينا حدث عشوائي هو قطرات المطر والتي تمثل حجم العينة وهنا حجم العينة كبير.

➰ احتمالية حدوث الحدث في فترة زمنية قصيرة تتناسب مع طول تلك الفترة وبالتالي تقع الأحداث تبعاً لمعدلات زمنية.

➰ احتمال حدوث أكثر من حدث واحد في فترة زمنية قصيرة جدًا هو صفر. فهو حدث نادر الوقوع.

➰ احداث مستقلة عن سابقاتها.

3. خلال تجربة معملية، متوسط عدد الجسيمات المشعة التي تمر من عداد.

نوع التوزيع: التوزيع بواسون لأنه يتميز بالخصائص التالية: (النعيمي وطعمة، 2020، ص 109)

➰ لدينا متغير عشوائي (عدد الجسيمات) يمكن أن يأخذ أي قيمة ضمن نطاق معين. ولايهم عدد الاحتمالات وفق بواسون.

➰ مرور الجسيمات المشعة له نفس احتمال المرور في هذه التجربة. (عدد الجزيئات التي تمر من العداد)

➰ كل حدث مستقل فكل جسيم يدخل في العداد مختلف عن الذي سبقه.

➰ الانحراف المعياري معروف. فالتوزيع مستمر والنتيجة محدودة بواسطة المعلمة التي نعتمدها، فهناك فاصل زمني بين مشعين، فطول الفترة يتحدد من الفرق بين الحدود، وهي جميع الفترات التي نفس طول الفترة

التمرين الثاني.

خلال ساعات العمل، يبلغ متوسط عدد المكالمات التي تمر عبر نظام ترحيل خلوي معين خمسة مكالمات في الدقيقة

جد ما يلي:

نوع التوزيع: توزيع بواسون(النعيمي وطعمة، 2020، ص 109)

السبب:

· لدينا حدث عشوائي (مرور مكالمة) يمكن أن يحدث في أي وقت. فيمكن أن تمر مكالمة أو لا تمر في أي وقت.

· احتمالية حدوث الحدث (مرور مكالمة) في فترة زمنية قصيرة (دقيقة) ثابتة.

· الأحداث مستقلة عن بعضها البعض. حيث لا تتأثر احتمالية مرور مكالمة بمرور مكالمات أخرى.

· احتمال حدوث أكثر من حدث واحد (مكالمة) في فترة زمنية قصيرة جدًا هو صفر.

وبالتالي تم اختيار توزيع بواسون لأنّه ينطبق على شروط المسألة.

- أوجد احتمال عدم مرور أي مكالمة عبر نظام الترحيل خلال دقيقة معينة

· متوسط ​​عدد المكالمات في الدقيقة (λ) = 5

· عدد الدقائق (t) = 1

بما أن التوزيع بواسون يمكن حساب احتمال عدم مرور أي مكالمة من خلال برنامج R بتطبيق الكود التالي: من أجل 5 مكالمات في الدقيقة:  

>dpois(0,lambda=5)enter

فيكن الناتج : 0,006737947 وهو احتمال عدم مرور أي مكالمة عبر نظام الترحيل خلال دقيقة معينة.

أوجد احتمال عدم مرور أي مكالمة عبر نظام الترحيل خلال فترة دقيقتين

🔔 متوسط ​​عدد المكالمات في الدقيقة (λ) = 5

🔔 عدد الدقائق (t) = 2

🔔 احتمال عدم مرور أي مكالمة: من أجل دقيقتين يكون عدد المكالمات 10 دقائق، وبالتالي في برنامج R، نكتب

>dpois(0,lambda=10)enter

فيكن الناتج 4.539993e^-05

 أوجد احتمال مرور ثلاث مكالمات عبر نظام الترحيل خلال فترة دقيقتين

🔔 متوسط ​​عدد المكالمات في الدقيقة (λ) = 5

🔔 عدد الدقائق (t) = 2

🔔 عدد المكالمات المرغوب فيها (k) = 3

🔔 احتمال مرور ثلاث مكالمات: من خلال برنامج R نكتب

>dpois(3,lambda=10)enter

قيكون الناتج 0.007566655 وهو احتمال مرور ثلاث مكالمات عبر نظام الترحيل خلال فترة دقيقتين:

ويمكن توضيح الحسابات السابقة كما في برنامج R من خلال المخطط التالي:

المراجع.

1. النعيمي، محمد عبد العال وطعمة، حسن ياسين. (2020). الإحصاء التطبيقي. عمان: دار وائل للنشر والتوزيع. تم الاسترجاع من الرابط https://platform.almanhal.com/Details/Book/95.
2. طويطو، محمد. (2017). مطبوعة خاصة بمقياس الإحصاء 3. موجهة لطلبة السنة الثانية ليسانس جميع الشعب. كلية العلوم الاقتصادية والعلوم التجارية وعلوم التسيير. جامعة الجزائر 3.