أنماط التعلم - ما هي أنماط التعلم لدى المتعلمين

ما هو مفهوم المجموعات؟

المجموعة (Set) هي واحدة من المفاهيم الأساسية في الرياضيات. وتُستخدم لتجميع عناصر متشابهة أو مرتبطة ببعضها وفقًا لخاصية محددة.

بمعنى آخر المجموعة هي تجمع من العناصر (أشياء. أعداد. رموز. ...) تُعتبر ككيان واحد.

اقرأ أيضاً المنطق الرياضي في الرياضيات المتقطعة - كيف تشتغل الترموستات؟

اقرأ أيضاً المنطق الرياضي - ما هي أدوات الربط في المنطق الرياضي؟.

🔓 يُشار إلى المجموعات عادةً بحروف كبيرة مثل A,B,C,…A,B,C,…. بينما يُرمز لعناصرها بحروف صغيرة مثل a,b,c,…a,b,c,….

🔓 إذا كان العنصر x ينتمي إلى المجموعة A. نكتب x∈A.

🔓 إذا لم يكن y عنصرًا في A . نكتب y∉A.

ما هي العلاقات بين المجموعات في الرياضيات؟

لندرس الحالة التالية : لتكن U= {1,2,3,4,5} . A={1,2,3} and B = {2,3,4}

أولاً -  صف العلاقات بين كل من هذه المجموعات. استعمل كلماتك الخاصة

لدينا ثلاث مجموعات ( U) و ( A) و ( B) وتلك العلاقات بين هذه المجموعات يمكن وصفها كما يلي:

1. العلاقة بين ( A) و ( U):

مجموعة ( A) هي جزء من المجموعة الشاملة ( U) لأن كل عنصر في ( A) (وهي الأعداد 1 و 2 و 3) هو عنصر أيضًا في ( U) (التي تحتوي على الأعداد 1، 2، 3، 4، 5). هذا يعني أن ( A ⊆ U) أي أن ( A) هي مجموعة جزئية من ( U) (قدسية، 2018، ص11).

2. العلاقة بين ( B) و ( U):

مجموعة ( B) هي أيضًا جزء من المجموعة الشاملة ( U). حيث أن كل عنصر في ( B) (وهي الأعداد 2 و 3 و 4) هو أيضًا عنصر في ( U). بالتالي. (U ⊇B) أي ان B هي مجموعة جزئية من U.

3. العلاقة بين ( A ) و ( B ):

يمكننا القول ان هناك بعض التداخل والاشتراك بين عناصر المجموعتين (A) و (B). حيث يشتركان في العناصر 2 و 3. ولكن كل من المجموعتين يحتوي أيضًا على عناصر خاصة به. فمثلاَ المجموعة (A) تحتوي على العدد 1. وهو غير موجود في المجموعة (B).

بينما المجموعة (B) تحتوي على العدد 4. وهو غير موجود في المجموعة (A). هذا يعني أن تقاطع (A) و (B) هو ( {2, 3} ) أي العناصر المشتركة بين المجموعتين. بينما اتحاد ( A ) و ( B ) هو ( {1, 2, 3, 4} ) وهو العناصر المشتركة وغير المشتركة.

ملخص العلاقات:

U ⊇A

U ⊇B

B ⋂ A =  {2, 3}

B ⋃ A ={1,2,3,4 }

ثانياً -  صف العلاقات بين هذه المجموعات مستعملاً الرموز الرياضية (الجمل !)

يمكننا وصف العلاقات بين المجموعات ( U ) و ( A ) و ( B ) باستخدام الرموز الرياضية:

وبالاعتماد على المجموعات المفوضة سابقاً وهي: U= {1,2,3,4,5} . A={1,2,3} and B = {2,3,4}

1. العلاقة بين ( A ) و ( U ):

U ⊇A أي أن كل عنصر في ( A ) هو أيضًا عنصر في ( U ).

2. العلاقة بين ( B ) و ( U ):

U ⊇B أي أن كل عنصر في ( B ) هو أيضًا عنصر في ( U ).

3. العلاقة بين ( A ) و ( B ):

🔑 التقاطع (العناصر المشتركة بين ( A ) و ( B )): B ⋂ A =   {3, 2}

🔑 الاتحاد أو الاجتماع (جميع العناصر التي تنتمي إلى ( A ) أو ( B )): B ⋃ A ={4,3,2,1 }

🔑 الفرق (العناصر التي توجد في ( A ) ولكن ليست في ( B )): B - A = {1} أي A\B = 1

والعكس: A - B = {4} أي B\A = 4

وبالتالي فإن ملخص العلاقات بالرموز:

U ⊇A

U ⊇B

B ⋂ A ={3, 2}

B ⋃ A ={4,3,2,1 }

B - A = {1} أي A\B = 1

A - B = {4} أي B\A = 4

📌 نُرشح لك هذا المرجع العلمي القيم: كتاب «الرياضيات المتقطعة لطلبة العلوم والحاسوب». 

                                                              حمّله الآن من هنا 👇

تحميل

3- نريد أن تكون مجموعة S=Ac ∩B. ما هي S؟ (تلميح ! الرمز Ac هو المتمم للرمز A )

لحساب المجموعة ( S = A^c ∩ B ) (حيث ( A^c ) هو متمم المجموعة ( A )). يمكننا اتباع الخطوات التالية:

1. حساب متمم ( A ) داخل المجموعة الشاملة ( U ):

متمم ( A ) يعني جميع العناصر في ( U ) التي ليست في ( A ).

بما أن ( A = {1, 2, 3}} ) و ( U = {1, 2, 3, 4, 5}} ). فإن:

A^c = U – A = {4, 5}

2. التقاطع بين ( A^c ) و ( B ): نأخذ الآن تقاطع ( A^c ) مع ( B ).

B = {2,3,4} و A^c ={4,5} . العناصر المشتركة بينهما هي: B ⋂ A^c ={4}

إذن. المجموعة S = B ⋂ A^c

هي: S = {4}

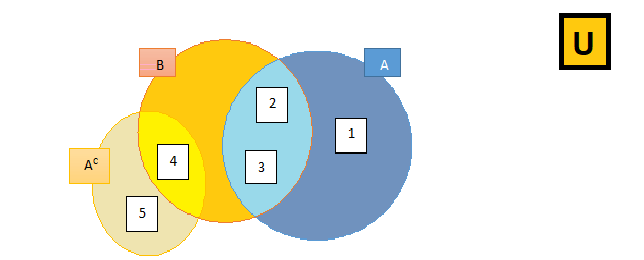
رابعاً -  ارسم مخطط فن للرمز S.

ما معنى مخطط فن؟

تستعمل مخططات فن لتسهيل التعامل مع مختلف المجموعات. حيث يمثل ما في داخل المستطيل عن المجموعة الشاملة Ω. وتمثل الدوائر الموجودة داخل المستطيل إلى المجموعات الأخرى (قدسية، 2018، ص12).

خامساً - كم عدد عناصر المجموعة P(U) اشرح لماذا؟

المجموعة ( P(U)) هي مجموعة جميع المجموعات الفرعية (أو المجموعات الجزئية) للمجموعة ( U). لتحديد عدد عناصر P(U) . يجب علينا أولاً معرفة عدد العناصر في المجموعة ( U).

في هذا السياق. المجموعة (U) هي { 1,2,3,4,5}. وبالتالي تحتوي على 5 عناصر.

كيفية حساب عدد عناصر P(U):

🔔 عدد العناصر في ( U) هو 5.

🔔 عدد المجموعات الفرعية لمجموعة: إذا كانت المجموعة تحتوي على (n) عناصر. فإن عدد المجموعات الفرعية لهذه المجموعة هو ( 2n). (الأشهب، 2024، ص48).

- في هذه الحالة. ( n = 5). لذا. عدد المجموعات الفرعية هو (25).

🔔 حساب (25): (25) = 2*2*2*2*2 = 32

إذن. عدد عناصر المجموعة P(U) هو 32.

لماذا يكون العدد هكذا؟

1. كل عنصر في المجموعة (U) يمكن أن يكون إما في مجموعة فرعية معينة أو لا يكون فيها. لذا. لكل عنصر في المجموعة (U). لديك خياران (إما أن يكون في المجموعة الفرعية أو لا يكون فيها).
2. بما أن هناك 5 عناصر في المجموعة (U). فإن عدد الطرق لاختيار أي مجموعة فرعية من بين هذه العناصر هو (25). وهذا يعطيك 32 مجموعة فرعية مختلفة.

إذاً. مجموعة المجموعات الفرعية P(U) تحتوي على 32 مجموعة فرعية.

المراجع.

1. الأشهب، سليم شفيق. (2024). الرياضيات المتقطعة لطلبة العلوم والحاسوب. دار المناهج للنشر والتوزيع. ملف pdf. منصة المنهل. تم الاسترجاع من الرابط https://platform.almanhal.com/Details/Book/36320.
2. قدسية، رامز. (2018). الجبر الرياضي. من منشورات الجامعة الافتراضية. دمشق. سوريا.

--------------------------------------------------------

مجلة التعلم

إن مجلة التعلم هي وسيلة لنتمكن من التعبير عن مشاعرنا نحو الدرس، وماهية المشاكل التي تواجهنا كطلبة في كل مساق، ومن خلالها يمكننا توضيح المشاكل التي تغلبنا عليها

في هذا الأسبوع تعلمنا بعض الحقائق في عالم الرموز الرياضية ونظرية المجموعات. هذه الوحدة كانت مليئة بالاكتشافات والتحديات،

حيث إن مجلة التعلم تعتبر وسيلة رائعة للتعبير عن التجارب والمعرفة التي اكتسبتها خلال الدرس. وسأقوم من خلال هذه المجلة بتوضح مشاعري وأفكاري حول بعض ما تعلمته خلال هذا الأسبوع. يمكنني أن أعبر عن العديد من الأمور التي تعلمتها وما هي تجاربي الشخصية. لذا سأركز على النقاط التالية:

- قبل هذه الوحدة، كنت أعتقد أن الرياضيات مجرد أرقام وحسابات. ولكنني اكتشفت أن هناك عالماً أوسع بكثير، عالم الرموز التي تمثل أفكاراً مجردة. تعلمت الكثير عن نظرية المجموعات، وكيف يمكن استخدامها لوصف العلاقات بين الأشياء المختلفة.

وبالتالي فالمعلومات التي لم أكن أعرفها من قبل، أذكر أهمية الرموز الرياضية الأساسية في فهم العلاقات الرياضية.

1. المعلومات التي كانت مغايرة لاعتقاداتي السابقة، أذكر أهمية طرق استخدام نظرية المجموعات في حل المشكلات الرياضية. فقد كنت أعتقد أن الرموز الرياضية جامدة وثابتة، ولكنني أدركت أنها يمكن أن تكون مرنة جداً وتستخدم لوصف مجموعة واسعة من الظواهر وتقوم بحل الكثير من العمليات الرياضية المنطقية. كما أنني تفاجأت بجمال بعض البراهين الرياضية، وكيف يمكن أن تكون بسيطة وأنيقة في نفس الوقت. حيث لاحظت أن نظرية المجموعات تدعم نظرية قواعد البيانات والبرمجة المنطقية، وتوفر اللغة لمناقشة الخوارزميات وحل التعقيدات والمشكلات الحسابية (فاستر كابيتال، 2024).
2. ساعدتني المناقشات والواجبات في تعلم معلومات جديدة من خلال التفاعل مع زملائي ومشاركة الأفكار. حيث عن المناقشات مع زملائي كانت مفيدة جداً، وقد ساعدتني في فهم بعض المفاهيم الصعبة. كما أن الواجبات الكتابية واسئلتها دفعتني إلى التفكير بشكل أعمق في المواد التي تعلمتها.
3. أكثر ما أثار اهتمامي هو تطبيق نظرية المجموعات في مجالات أخرى مثل علوم الكمبيوتر والاحتمالات. أود أن أعرف المزيد عن كيفية استخدام هذه النظرية لحل المشكلات الواقعية.
4. واجهت بعض الصعوبات في فهم بعض البراهين الرياضية الطويلة والمعقدة. وبعض التحديات التي اعترضت طريق الفهم لتلك المفاهيم، ولكن مع الممارسة والمناقشة مع زملائي، تمكنت من التغلب على هذه الصعوبة.
5. الأشياء التي أدركتها عن نفسي وأسلوب تعلمي، هي قدرتي على التحمل والصبر واستخدام العديد من المهارات للتوصل إلى حل المسائل الصعبة. وقد أدركت أنني أحتاج إلى المزيد من الصبر والمثابرة لفهم المفاهيم الرياضية المعقدة. وأيقنت أهمية العمل الجماعي والتعاون مع الآخرين في عملية التعلم.
6. كانت تعليقات زملائي مفيدة جداً، وقد ساعدتني في تصحيح بعض الأخطاء التي كنت أرتكبها. كما أنها شجعتني على بذل المزيد من الجهد. ولا أنسي شعوري حيال التعليقات من زملائي، كالفرح بالملاحظات الإيجابية والاستفادة من النقد البناء لتحسين أدائي في المستقبل.

مما سبق نجد أنه باستخدام مجلة التعلم، يمكنني تنظيم أفكاري وتسجيل تقدمي الشخصي في الدراسة، مما يساعدني على تعزيز فهمي ومهاراتي التعليمية. حيث كانت هذه الوحدة تجربة غنية بالتعلم والتحديات. وأنا متحمس لمواصلة استكشاف عالم الرياضيات.

المراجع.

1. فاستر كابيتال. (2024). نظرية المجموعات: كشف أسرار نظرية المجموعات من خلال مخططات فين. منصة فايستر كابيتال. تم الاسترجاع من الرابط https://2u.pw/Dhbjf .