ما هو مفهوم المنطق الرياضي؟
المنطق الرياضي هو الأساس الرياضي الذي يتم الاعتماد عليه في علوم الحاسوب، ومن أجل فهم الرياضيات لابد من فهم ما يبرهن على حقيقية رياضية وأن تكون الحجة الرياضية صحيحة.ما هو مفهوم الفرضية؟
بينما الفرضية هي جملة خبرية قد كون صحيحة وقد تكون خاطئة، ولكن ليس الاثنان معاً.ما هو جدول الصواب؟
هو أداة تُستخدم في المنطق لتحليل صحة أو خطأ العبارات المنطقية بناءً على قيمها الصوابية (True أو False). يُستخدم لتوضيح النتائج الممكنة للعمليات المنطقية بعض الأدوات المنطقية مثل "و" (AND) و "أو" (OR) و "ليس" (NOT) والعبارات الشرطية. (الجبوري والمفرجي، 2024، ص26).في هذه الوحدة، درسنا المنطق الفرضي للأثبات. وكذلك درسنا جدول الصواب. من خلال مصادر واجب القراءة مثل (الأشهب، 2024). (قدسية، 2018).
يمكننا إنشاء جدول الصواب بتحديد العبارات البسيطة اولاً حيث نبدأ بتحديد العبارات المنطقية البسيطة مثل (P) و (Q). ومن ثم حساب التوليفات الممكنة.
فلكل عبارة، هناك حالتين: صواب (T) أو خطأ (F). وإذا كان لدينا عبارتين، فإن عدد التوليفات الممكنة هو ( 2^n )، حيث ( n ) هو عدد العبارات. على سبيل المثال، في حال كان لدينا العبارتين، (P) و (Q)، ستكون التوليفات 4 وهي:
- ( P ) صواب، ( Q ) صواب
- ( P ) صواب، ( Q ) خطأ
- ( P ) خطأ، ( Q ) صواب
- ( P ) خطأ، ( Q ) خطأ
ثم نقوم بإضافة العمليات المنطقية في كل صف من التوليفات، بأن نقوم بحساب نتيجة العملية المنطقية التي نرغب في تحليلها.
على سبيل المثال، العملية التي تعتمد ( "و" (AND)). يكون الناتج صوابًا فقط إذا كانت كلا العبارتين صواب. أما العملية التي تعتمد ("أو" (OR))، فيكون الناتج صوابًا إذا كانت واحدة على الأقل من العبارتين صواب. (الجبوري والمفرجي، 2024، ص27).
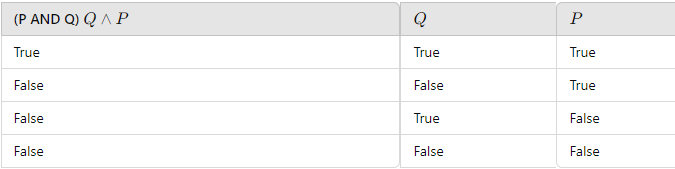
مثال بسيط: إذا كان لدينا العبارتان (P) و (Q):
في هذا المثال، نتيجة ( P ∧ Q ) تكون صوابًا فقط في حالة واحدة وهي عندما تكون ( P ) و ( Q ) كلاهما صواب. وعكس ذلك يكون خطأ.
ما هي المعلومات التي لم تكن تعرفها من قبل؟
عند التفكير في المنطق الفرضي وجدول الصواب، هناك بعض الجوانب التي قد تكون جديدة أو غير متوقعة، وأحد هذه المفاهيم الجديدة والتي تعلمتها هو كيفية استخدام جدول الصواب لتقييم صحة العبارات المنطقية المركبة.فقد كنت أعرف بعض المبادئ الأساسية، ولكن طريقة انشاء جدول شامل ومتكامل لكل التوليفات الممكنة من القيم الصوابية للعبارات الفردية كان فكرة جديدة بالنسبة لي، كما كانت مفيدة لتحديد مدى صحة الافتراضات المنطقية.
ما هي المعلومات التي تعتبرها مغايره لما كنت تعتقد؟
كنت أعتقد أن إثبات صحة الافتراضات يعتمد فقط على الحدس أو الفهم العام للمنطق، إلا انني اكتشفت وجود نظام مرتب مثل جدول الصواب الذي غيّر منظوري. حيث إن هذه الأداة توفر طريقة منهجية لحل مسائل منطقية بدون الاعتماد فقط على التخمين أو الحدس.كيف ساعدتك المناقشة و / أو الواجبات في تعلم معلومات جديدة؟
المناقشات والواجبات ساعدتني في تطبيق المفاهيم بصورة عملية. على سبيل المثال، عندما نقوم بحل مسائل إثباتية أو إنشاء جدول الصواب لمختلف العبارات، فإننا نلاحظ وندرك الفروق الدقيقة بين العبارات الشرطية والمقابلات الثنائية مثل "و" و "أو".أي من المواد جعلتك ترغب في معرفة المزيد عنها؟
الموضوع الذي قد يكون أثار اهتمامي أكثر هو كيفية استخدام المنطق الفرضي في الحياة الواقعية أو البرمجة. والقدرة على تحليل العبارات المنطقية ومحاولة إثبات صحتها باستخدام الجداول أو الرموز مما حفز لي الرغبة في معرفة المزيد عن التطبيقات العملية لهذه المهارات، خاصة في مجالات مثل الذكاء الاصطناعي أو التحليل الرياضي.هل واجهتك اشياء صعبه أو تحديات؟
بالفعل واجهتني صعوبة في البداية حول فهم كيفية بناء جدول الصواب بشكل صحيح. تحديد جميع التوليفات الممكنة للقيم الصوابية ومتابعة كل خطوة في الإثبات، ولكن مع التكرار والممارسة أصبح الأمر أكثر يسراً.ماذا أدركت عن نفسك وعن أسلوب التعليم الخالص بك؟
لقد أدركت أنني أتعلم بصورة أفضل من خلال التطبيق العملي والتجربة. حيث أعطتني المناقشات والواجبات فرصة لاستخدام المفاهيم بطريقة ملموسة، مما عزز فهمي بشكل أفضل مما لو درست المفاهيم النظرية فقط.كيف كان شعورك حيال التعليقات التي حصلت عليها من زملائك؟
إذا حصلت على تعليقات بناءة من زملائي، سوف أشعر بالتقدير والتحفيز. فالتعليقات قد تكون مساعدة على تحسين فهمي وتصحيح أي أخطاء في معلوماتي. كما أنها قد تجعلني أشعر بالثقة في تطبيق المفاهيم، خاصة إذا كانت إيجابية وداعمة.في الختام نحتاج للتعلم باستمرار وكل أسبوع أجد أن واجباته زادت من معارفي في الرياضيات عن الأسبوع السابق.
المراجع.
- الأشهب، سليم شفيق. (2024). الرياضيات المتقطعة لطلبة العلوم والحاسوب. دار المناهج للنشر والتوزيع. ملف pdf. منصة المنهل. تم الاسترجاع من الرابط https://platform.almanhal.com/Details/Book/36320 .
- الجبوري، محمد هادي والمفرجي، ناصر حسين سلمان. (2024). الرياضيات المتقطعة في علم الحاسوب. منصة المنهل. ملف pdf. تم الاسترجاع من الرابط https://platform.almanhal.com/Details/Book/121.
- قدسية، رامز. (2018). الجبر الرياضي. من منشورات الجامعة الافتراضية. دمشق. سوريا.